Synth

I am trans and autistic, of course I have made my own synth. For reasons of affordability, practicality, modularity, and experience, I decided to make it a software synthesizer.

This page is divided in two parts: Theory, where I explain fundamentals of audio synthesis, and Practice, where I go over exactly how my synthesizer works.

Theory

“Sound” is vibrations in the air, in this case produced by a loudspeaker (a plastic membrane moved around via magnetic induction). Under gnu/linux, the aplay command gives us a convenient way to control those movements - the program reads data and sets the position of the loudspeaker - in the default configuration, it reads a single byte (a number between 0 and 255) (generally called a sample - though ‘sample’ is also often used to refer to a recording) 8000 times a second (sampling rate), and sets the membrane’s position to roughly correspond to the position of that value between its extremes (amplitude). Our job, then, is to figure out where to put it at different times (this is kept track of by a timestamp - in our case, a number we increment with every byte we output).

Tone generation

First off, to synthesize anything, we need to be able to make tones in general. We have a couple optoins there.

Sine wave

Tones - sounds in general - usually follow either a simple sine wave, of the type you know from those dreadful math lessons in middle and high school, or a combination of sine waves. They are the foundation of most sound synthesis.

   ,_
 /   `.
'      \     /
        `._,'
Fig. 1 - rough approximation of a sine wave.

Square wave

While sine waves may be the most ‘natural’, they are rather ‘mathematical’ in nature, and thus not very intuitive for computers. Early computers used something much more intuitive, called a square wave - either high (bit value 1) or low (bit value 0), switching quickly between the two - if displayed on an oscilloscope, this makes them look like squares, giving them their name.

 _____
|     |
|     |     |
      |_____|
Fig. 2 - a square wave

By using a neat little trick called pulse-width modulation, we can shift around the relative thicknesses of the squares, giving the sound different qualities. _ _ | | | | | | | | | || || Fig. 3 - a low-PWM square wave

Triangle and sawtooth waves

Square waves are nice and all, but can sound quite grating (which can be charming imo, but still). It was soon after that hardware had advanced enough to let us put the sharp corners somewhere else, approximating sine waves much better with something called a triangle wave.

  /\
 /  \
/    \  /
      \/
Fig. 4 - a triangle wave

Shifting the peaks all the way forward or back, we get something between a triangle and a square wave. Keeping with the visuals, it’s called a sawtooth wave.

    .    .  .    .
   /|   /|  |\   |\
  / |  / |  | \  | \
 /  | /  |  |  \ |  \
/   |/   |  |   \|   \
Fig. 5 - a back- and a front-weighted sawtooth wave

FM synthesis

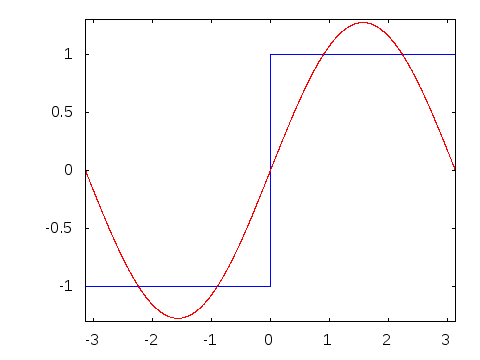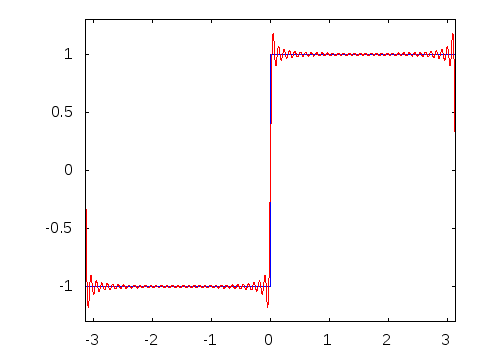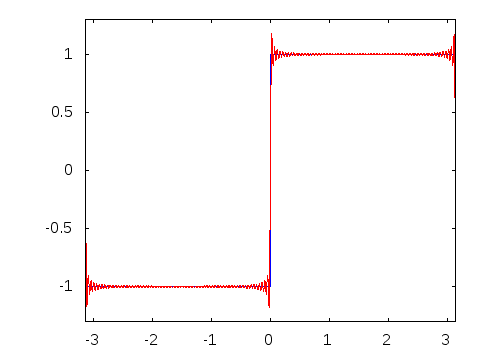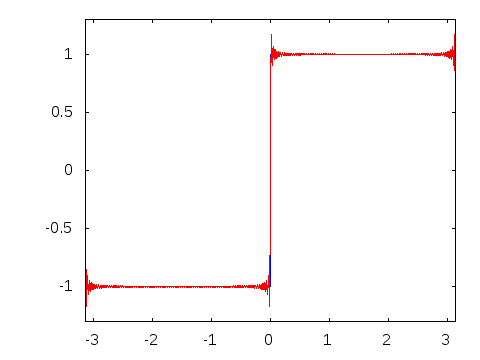
As mentioned in the segment on sine waves, all sound is a combination of sine waves. This is also true for the other waves listed above - while they are easier to generate directly, we can also generate them from summing up sine waves of different frequencies and amplitudes. For example, a square wave is the sum of odd overtones with proportionately decreasing amplitude - to generate a square wave of a given frequency, we start with a sine wave of that frequency, we then add a wave with three times the frequency and a third of the volume, then five times the frequency and a fifth of the volume, etc etc. As we keep adding more waves, the result gets closer and closer to a square wave.

XXX include graphic

Equal temperament XXX

Noise

And let’s not forget that if we just output random numbers, we’ll get something called white noise. It’s an even mix of frequencies, therefore sounding like nothing in particular (musically speaking - in practice it sounds a lot like rumbling steam, or a wind blowing through gaps). While it might sound useless at first to make sound that sounds like nothing, this is surprisingly useful - we can use filters to modulate it into different kinds of noise, and a smidgeon of brown noise is just what is needed to give that drum sound the right feel.

Filters

As promised, filters - specifically, frequency filters, of the low-pass and high-pass variety. The sample amplitude/loudspeaker position/air pressure/etc changes between samples, and by twiddling with the amount of change, we can mess around with the frequencies it has.

Let’s say we have a sample s, and also keep track of the sample before it, called s_prev. We also take a filter parameter a (and assume all of them are between 0 and 1). The following equation describes a frequency filter:

s=s_prev+(s-s_prev)*a

s-s_prev is the difference between the current and the previous sample. If a=1, we add the full difference to the previous sample, resulting in no change to the sound. If however we only add a bit of it (say, a=.5), then quick changes to the sound will get muted out, while slow and gradual ones will remain mostly unchanged. We have thus created a low-pass filter.

We can create a high-pass filter by making a low-pass one and subtracting it from the sample - thus, we remove the low frequencies while keeping the high ones.

s=s-(s_prev+(s-s_prev)*a) =s-s_prev-(s-s_prev)*a =s-s_prev+(s_prev-s)*a =(s-s_prev)*(1+a)

A low-pass and a high-pass filter can then be combined to form something called a band-pass filter, letting only the frequencies between them pass.

reverb

Envelopes

Ah yes, the good ol' ADSR envelope. While the above lets us generate tones that sound “like an instrument”, they only do so while the instrument is making the sound - it goes from 0 to 100 and then right back to 0, not accounting for the sharp hit of piano keys or the gentle fade of bells. This is where envelopes come in - modifying the frequency and amplitude of sounds to make them sound like they were produced by actual instruments.

“ADSR” stands for “attack - decay - sustain - release”. The four roughly describe the four stages of a note being played - the sharp onset, the following drop to its base amplitude/frequency (in reality an exponential decay, but often modeled as linear for practical reasons), and the fade-out when the note is released. Playing around with these values can be used to model a plethora of instruments - a quick and high attack, followed by a quick delay and a low sustain, makes for a good arpeggio, and a long delay with no sustain makes a drum.

   a
  aaddd
 aaadddsssssssr
aaaadddsssssssrr
Fig. 6 - rough plot of note amplitude

The “issue” (at least for us) with envelopes is that one needs to know when the note is being played - if we only have the tone of it, this can get tricky to figure out. Most modular synthesizers use a “trigger” signal to set off a note, which can then also be fed into any envelopes and effects that need to know. We will use the fact that notes are tied to a base rhythm, generate envelopes for that, and modulate the notes with those.

voice synthesis

A neat little trick we can do (but won’t) is voice synthesis - literally, making the computer speak.

Trackers

Trackers are a rather simple concept - a list of notes, and when to play them. A list of trackers, combined with a sineave generator, already makes for a functioning sound system - albeit a very basic one. A couple of them can be used to make a decent synth - the NES used two square wave [], one for triangle waves, and one for noise.

Practice

This section deals wth the how of the synthesizer.

The synth reads a file telling it how to make the sounds it is supposed to, and then enters an endless loop. Each iteration increments a variable t, telling us how much we’ve played - we use it to index tracks and generate waves.

Melody and program separation

The first part of the file contains tracks - sequences of characters representing values, mainly intended to be used as notes to play. We will use ASCII to represent a piano keyboard - matching the 49th character (1) to the 49th key, we get the following equivalence (the space character is used to signify a pause - it would’ve otherwise come before the exclamation mark):

       !"#$%&'
 ()*+, -./0123
 45678 9:;<=>?
 @ABCD EFGHIJK
 LMOPQ RSTUVWX
||_|_|||_|_|_|||_|_||
|_|_|_|_|_|_|_|_|_|_|

XXX melody memory management

The : character signifies the beginning of the program, the ‘$’ its end - this unfortunately also means we cannot have a melody starting with a 2d#, but that ends up being negligible (having the program start on two newlines would circumvent that, but also that sounds like effort). The program is a list of instructions, each telling us how to manipulate memory, in the end resulting in the tone to output.

single-token reverse polish (stack-based) notation

The program language is made to be as easy to interpret as possible - each command is a single character long (meaning we don’t need much in way of parsing), and operates on a stack (meaning each command takes and returns a specific number of arguments, so we don’t need any extra context to keep track of that). For the nerdy among you - this is the ontological opposite of the lisper, where the majority of work lay in the parsing, because we used a lot of brackets to denote what function belongs with what arguments.

To elaborate: “stack” means we have a list of values. Commands take elements from the end (known as a pop, do stuff with them, and put the result back at the end of the list (known as a push). Since each command always pops and pushes the same number of arguments, we just need to make sure the right arguments are at the top of the stack when we use a function, and we know its result(s) will be on top when it finishes.

Command list

Now, for the actual commands we’ll be using: - 0123456789abcdef - all push their value (as read in hexadecimal) on the stack. - \`` - takes the two uppermost values, and pushes them back as a 8-bit integer (since the previous commands only let us input numbers 0-15 when the synth uses values 0-255) -:- duplicates the uppermost value -/- swaps the uppermost values -!- takes the uppermost value and inverts it (subtracts it from 255) -*- takes the uppermost values and pushes their product (divided by 256 to renormalise it) --- takes the uppermost values and returns their difference -+- takes the uppermost valuen, then takes the average of the uppermostnvalues -~_%^- takes the uppermost value, read as a piano key, and generates a sine/square/sawtooth/triangle wave with that frequency. Instead of explaining in length how that's supposed to work, here's the verbatim code: a=pop(); float freq = a==32?0:440*powf(2,(float)(a-49)/12); if(freq)push(sinf((float)t*freq*M_PI*2/rate)*127+127);else push(0); -t- takes two values, returns a note. The uppermost value tells it play speed (in eigths of a second), the second uppermost value tells it which track to read the value from. -z` - takes the uppermost value, returns a sawtooth wave over that many notes (iow period length is measured in eigths of a second, like above). This, combined with the inverter and product, can be used to make basic envelopes.

Examples XXX

(written 08052024, wip)